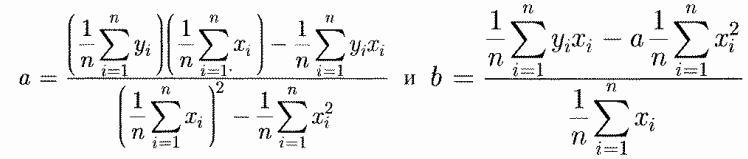Линейная регрессия в С++
Задача состоит в том, чтобы для набора случайных данных, а точнее для набора точек на плоскости построить прямую линию, которая наилучшим образом описывает эти данные. То есть проходит так, что сумма квадратов разности между точками прямой и точками из случайного набора данных минимальна. Теперь подробнее. Даны два набора данных:
$$X=\left\{x_{1},x_{2},x_{3},x_{4}...x_{n} \right\}, Y=\left\{y_{1},y_{2},y_{3},y_{4}...y_{n} \right\}$$
На плоскости эти наборы задают координаты точек. Теперь надо найти коэффициенты a и b прямой:
$$y=ax+b$$
причем прямая должна проходить так, чтобы выполнялось условие:
$$\sum_{1}^{n}{\left(a\cdot x_{i}+b-y_{i} \right)}^{2}\rightarrow min$$
Это условие минимизации суммарного расстояния между точками прямой и соответствующими точками из исходного набора данных.
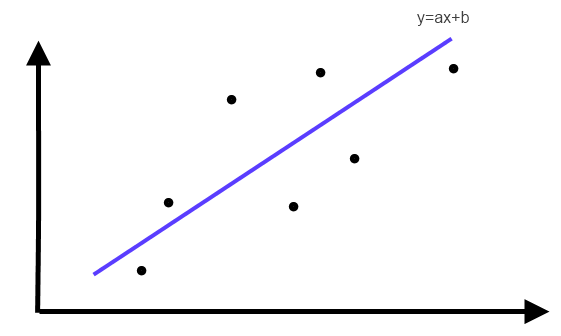
Пример такого решения приведен на рисунке справа - синим обозначена найденная прямая, а черными точками - точки для набора исходных данных. Если менять значения коэффициентов, то будет меняться расположение линии. Такая задача очень актуальна при обработке разных данных в самых разных областях: статистике. экономике, промышленности. Такая задача часто приводится в дипломных работах не только математиков или программистов в последней главе, где выполняется обработка результатов.
Чтобы получить формулы для определения неизвестных коэффициентов a и b линии регрессии поступают так: находят две частные производные от оптимизирующей функции, приравнивают их к нулю и решают систему уравнений. Полученные в результате выкладок формулы приведены на рисунке слева (кликабельно).
Регрессионная модель тем точнее описывает данные, чем ближе реальная статистическая зависимость между параметрами х и у к той функциональной зависимости, что использовалась при построении модели. Другими словами, чтобы статистические данные хорошо ложились на аппроксимирующую кривую, необходимо удачно подобрать вид этой кривой. К сожалению, точных методов для этого не существует. Внизу приведен листинг программы, которая решает указанную здесь задачу.
#includeusing namespace std; int main(){ //Размер массива: const int n=10; //Индексная переменная: int i; //Массивы статистических значений: double x[n],y[n]; //Параметры модели: double a,b; //Средние значения: double Sx=0,Sy=0,Sxy=0,Sxx=0; //Ввод статистических данных: cout << "x = "; for(i=0; i < n; i++) cin >> x[i]; cout << "y = "; for(i=0; i < n; i++) cin >> y[i]; //Вычисление параметров модели: for(i=0; i < n; i++){ Sx+=x[i]; Sy+=y[i]; Sxy+=x[i]*y[i]; Sxx+=x[i]*x[i]; } Sx/=n; Sy/=n; Sxy/=n; Sxx/=n; a=(Sx*Sy-Sxy)/(Sx*Sx-Sxx); b=(Sxy-a*Sxx)/Sx; //Результат: cout << "a = " << a << endl; cout << "b = " << b << endl; return 0; }