Интегрирование для продвинутых
Теперь вы можете не только получить точное или приближенное значение интеграла, но даже формулу для аппроксимации при вычислении интеграла. Это может быть полезно, если вам эта формула нужна для дальнейших исследований или использования. Для того, чтобы сразу понять о чем идет речь, просто введите в решатель строку, которую вы видите ниже и нажмите "Решить".
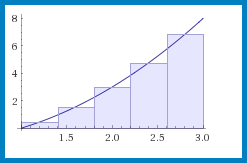
midpoint method of x^2-1 from 1 to 3На рисунке слева сверху приведена иллюстрация процесса вычисления по этому методу. Вы получите в результате не только численное приближенное значение интеграла, вычисленное методом прямоугольников с выбором средней точки, но и разложение в ряд, которое дает это самое приближенное значение.
Кроме того, что вы сможете посмотреть и подробно выкладки show details. Кроме того будет построен график абсолютной погрешности (или относительной), а также вы получите табличку со сравнением точности разных методов (см. рисунок) и даже с результатами вычисления с использованием других методов. Из рисунка легко догадаться, что можно получить значение интеграла и соответственно приближенное разложение интеграла разными методами. Приведем возможные варианты применения разных методов для вычисления интеграла на примере команд, список которых приводим ниже. Попробуйте их ввести в строку решателя и посмотреть на результаты. Как вы догадались, можно брать интегралы для разных функций и разных промежутков.
left endpoint method of x^2-1 from 1 to 3
right endpoint method of x^2-1 from 1 to 3
trapezoidal rule of x^2-1 from 1 to 3
Simpson's method of x^2-1 from 1 to 3
Boole’s rule of x^2-1 from 1 to 3Работая с этими командами для получения приближенных разложений, математики получат огромное удовольствие, анализируя быстро точность методов для вашей функции. Все это можно использовать, например, для выбора приближенного метода для той или иной функции или для получения разложений для функций для которых не существует символьной формы решения.