Создание бинарного дерева
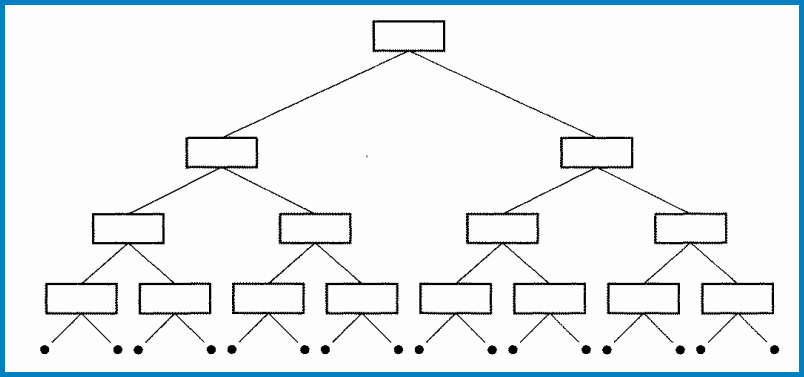
Структуры, используемые вместе с динамическими массивами, позволяют создавать сложные структурные образования, полезные при решении самых разнообразных задач. Здесь рассмотрим создание бинарного дерева.Под бинарным деревом в общем случае подразумевают структуру связанных данных, в которой каждый элемент указывает на два других элемента того же типа. В вершине иерархии находится один элемент (первый эле мент). Он связан с двумя другими элементами (элементы второго уровня). Каждый элемент второго уровня связан с двумя элементами третьего уровня и т.д. Если бинарное дерево состоит из N уровней (начальный уровень полагается первым), то на последнем уровне количество элементов равно \(2^{N-1}\), а общее количество элементов дерева равняется\(2^{N}-1\). Схематически бинарное дерево представлено на следующем рисунке.
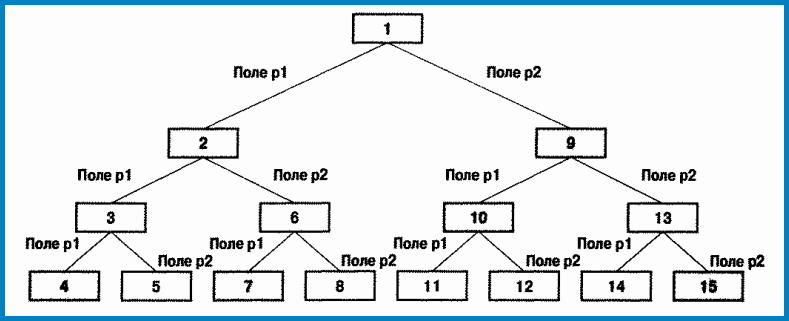
При создании бинарного дерева все элементы нумеруются. Для нумерации элементов дерева вводится глобальная переменная Count с нулевым начальным значением. При создании каждого нового элемента дерева значение переменной увеличивается на единицу Поэтому, например, чтобы узнать количество созданных элементов, достаточно проверить значение переменной Count. Элементами бинарного дерева являются переменные структуры BinTree. Структура описана как такая, что имеет три поля: два указателя р1 и р2 на структуры того же тина и целочисленное поле n. Значениями указателей присваиваются адреса тех элементов-структур, на которые ссылается данный элемент, в поле n записывается порядковый номер элемента. Порядок создания дерева показан на рисунке ниже.
#includeusing namespace std; //Счетчик элементов дерева: int Count=0; //Структура-элемент дерева: struct BinTree{ //Поля-указатели: BinTree *p1; BinTree *p2; //Целочисленное поле: int n; }; //Функция создания бинарного дерева: BinTree *MakeTree(int N){ //Указатель на создаваемый элемент: BinTree *p; p=new BinTree; //Создание дерева: Count++; p -> n=Count; if( N > 1 ){ p -> p1=MakeTree(N-1); p -> p2=MakeTree(N-1);} //Результат-указатель на созданный элемент: return p; } int main(){ //Указатель на нулевой (начальный) элемент: BinTree *q; //Создание 4-х уровневого бинарного дерева: q=MakeTree(4); //Проверка результата. Количество элементов: cout << "Elements in tree: " << Count << endl; //Элемент №1: cout << q -> n << endl; //Элемент №2: cout << q -> p1 -> n << endl; //Элемент №4: cout << q -> p1 -> p1 -> p1 ->n << endl; //Элемент №7: cout << q-> p1 -> p2 -> p1-> n << endl; //Элемент №9: cout << q -> p2 -> n << endl; //Элемент №10: cout << q -> p2 -> p1 -> n << endl; //Элемент №15: cout << q -> p2 -> p2 -> p2 -> n << endl; return 0; }