Основи тригонометрії: таємниці кутів та синусів
Тригонометрія: як розібратись?
Синуси та косинуси знайомі кожному, хто хоча б трошки вчився на уроках математики, а не просто просиджував їх в очікуванні інших предметів. І хоча, на перший погляд, тригонометрія видається не дуже потрібним розділом — це не так! Для майбутніх географів, астрономів, геодезистів і навіть військових необхідні знання з тригонометрії. Розберімось в основах разом!
Що таке тригонометричні функції?
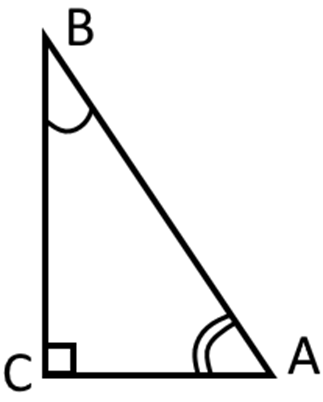
Найпростіші функції — це синус, косинус, тангенс та котангенс. Щоб зрозуміти, що це таке, потрібно намалювати прямокутний трикутник, позначити на ньому кути, визначити де в нас катети, де — гіпотенуза.
На зазначеному вище трикутнику AB — гіпотенуза, BC та AC — катети. Тепер розбираємося з функціями на прикладі кута А:
- Синус (sin) — це відношення протилежного катета до гіпотенузи. Катет, протилежний до кута А — ВС. Тобто, \(sin(A) = BC/AB\).
- Косинус (cos) — це відношення прилеглого катета до гіпотенузи. Прилеглим катетом в такому випадку є АС. Тоді \(cos(A)=AC/A\).
- Тангенсом (tg) — це відношення протилежного катета до прилеглого катета. \(tg(A) = BC/AC\).
- Котангенс (ctg) — протилежне тангенсу, відношення прилеглого катета до протилежного. \(ctg(A) = AC/BC\).
Кожна функція — це відношення різних сторін одна до одної. При цьому, кожен кут може мати значення як в градусах, так і в радіанах. Суть полягає в тому, що є певна закономірність цих значень, залежно від розміру кута. Якщо вам досі здається, що тригонометричні функції — це складно, допоможе репетитор математики. Він зможе пояснити незрозумілі моменти та допомогти навчитися розв’язувати не тільки прості, а й складніші тригонометричні функції.
Для деяких значень кута існує табличка, в які вказані найбільш часто вживані значення.
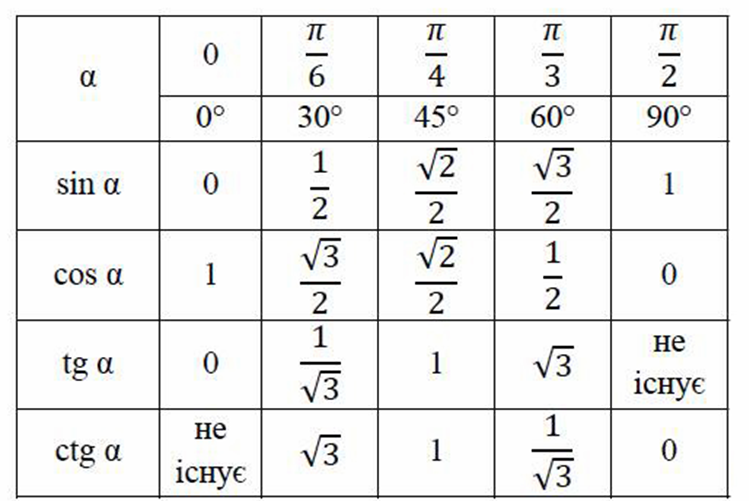
В синусі та косинусі є певна закономірність значень. Замість числа під коренем просто треба підставляти числа від 0 до 4 (для синуса) або у зворотному порядку від 4 до 0 (для косинуса).
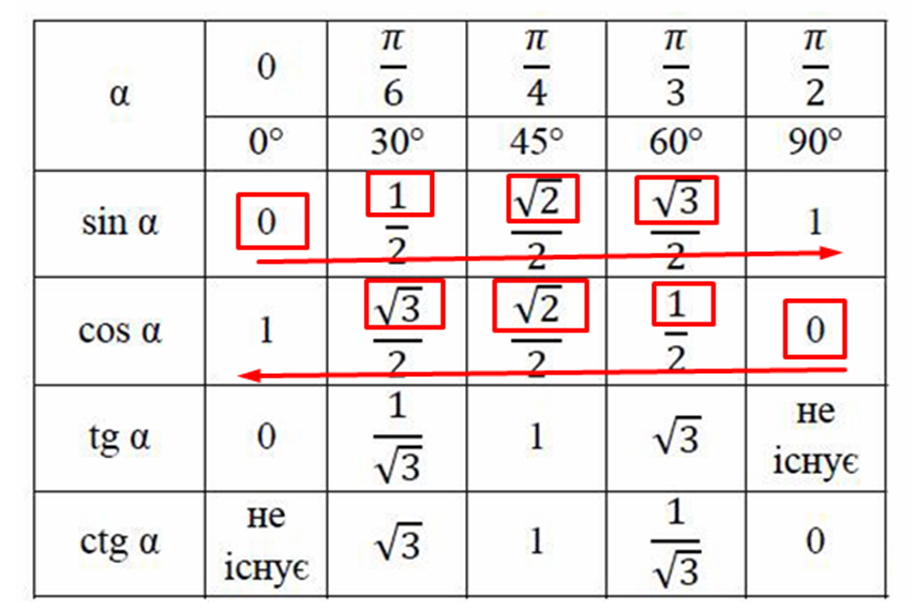
Оскільки функції синуса і косинуса є своєрідним віддзеркаленням, виникає головна тригонометрична властивість.
$$sin^2(x)+cos^2(x)=1$$
Вона легко підтверджується підставлянням будь-якого значення кута в рівняння та обрахуванням, тому можете спробувати.
Окрім цієї формули існує перелік ще декількох обов’язкових до вивчення формул з тригонометрії. Всі вони базуються на значенні синусів, косинусів, тангенсів, котангенсів, а також мірі кута.
$$tg\alpha=\frac{\sin\alpha}{\cos\alpha},\;\;ctg\alpha=\frac{\cos\alpha}{\sin\alpha},$$
$$tg\;a\;\cdot ctg\;a\;=\;1,\;a\neq\frac{\pi n}2,\;n\;\in\mathbb{Z}$$
$$1+tg^2a=\frac1{\cos^{2\;}a},\;a\neq\frac\pi2+\pi n,\;n\in\mathbb{Z}$$
$$1+ctg^2a=\frac1{\sin^{2\;}a},\;a\neq\pi n,\;n\in\mathbb{Z}$$
$$\sin2a=2\sin a\cdot\cos a$$
$$\sin^2a=\frac{1-\cos2a}2$$
$$\cos^2a=\frac{1+\cos2a}2$$
Щоб розібратися у формулах було простіше, на допомогу прийдуть репетитори геометрії. Тільки перевірені спеціалісти з фаховою освітою, які мають неперевершений досвід в освітній сфері допоможуть опанувати усі правила розв’язування тригонометрії. Не гайте час дарма — заходьте на сайт прямо зараз та знайдіть для себе ідеального викладача!

